СЕКУНДНЫХ РАБОТ ЕГО СИЛ И МОМЕНТОВ

При решении многих задач удобно применять для определения кру­тящего момента несущего винта выражение, которое можно получить, используя теорему об изменении кинетической энергии тела. На рис. 1.16 показан элемент лопасти и аэродинамические силы, действующие на него. Скорости перемещения элемента: в плоскости вращения — Ux, а по нор­мали к ней — Uу —уг ф, т. е. воздушная скорость без учета индуктивной. Секундная работа сил (малые силы трения и тяжести учитывать не будем)

dA = — dQnUx — dTn [Uy + УГф ]. (1.98)

Нетрудно показать, что dQnUx + dTn Uy = dXanU (так как d Yan LU, то ее работа равна 0). Следовательно,

dA = — dXanU — dT^. (1.99)

Со стороны втулки несущего винта на лопасть действуют силы и мо­менты — Н*, — Т*, — S’*’, — М* , (см. рис. 1.19). Отме-

л Н Z Н 1

Рис. 1.16. Силы, действующие на элемент лопасти и часть втулки

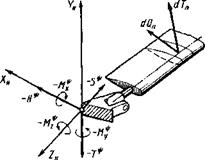ТИМ, что это суммарные силы и мо­менты, содержащие аэродинамичес­кую и инерционную части. Секунд­ная работа всех сил, действующих на лопасть,

А* = — / [dXanU +

О

+ dTSiyr^’ + НФ VXi[ —

— Т* Ууи -■ М£к шхн _

— М*н«>ун — MfH ш2н — (1.100)

При установившемся движении кинетическая энергия лопасти на равных фл одинакова, следовательно, интеграл от секундных работ равен нулю:

~ 7 J [dXajl и + dTnyr^ } — HVXW + TVyw +

2л О О

+ Мхн шхи + Мун ь)ун + М2Н согн = 0.

Так как мощность несущего винта N = MKсон =-Мун сон, то

N = ^проф + ^инд ~ ЯКХН + ТУул + MXYl сохн + MZH coZH,

(1.101)

к — 2 л її

Л^проф = — Г — S d4>n J dXajl U;

и ^ 2л о о

(1.102)

2 л Д

*инд = Ї dtn SdT„Vri.

2л о о

Таким образом, мощность несущего винта выражена как сумма се­кундных работ его сил и моментов и потерь на профильное и индуктив­ное сопротивление лопастей.

Уравнение (1.101) принято называть уравнением баланса энергии несущего винта. Оно часто используется в виде

N = ^проф + ^инд ~ ^а* н + шхн + ^гн wxh > (1.103)

где Ха*н = Г sin а н + ЯcosaH — сила сопротивления несущего винта. Когда скос потока у несущего винта мал, Ха* н ~ Хан.

В безразмерном виде эти уравнения записываются как

ткя ~~ ^проф + ^иид — + + тхя^хя +

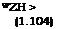
+ mZH ^zh — ^проф + тиня ~~ *хн V* + тхя ^хя + тгя

причем

1 1-а і ~ — _

^проф ~~ ~ / d*Pn / Cxp^rU dr,

2» О о

1 2п 1 _

^инд — ~ / <іфп fdtnvry.

2п о о, Y

Отметим, что последние два слагаемых выражений (1.103), (1.104) малы по величине и могут быть опущены.

Уравнение (1.103) можно получить и без применения теоремы об изменении кинетической энергии, а формально, путем преобразования выражений для гпкн. Для аэродинамической составляющей момента и при сохн = со2Н = 0 вывод приведен в работе [ 17 ]. С учетом toXH, со2н и при уточненных выражениях для тхи, mZH (1.81) … (1.83) получим

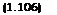d™кн. а ^^проф +^лгинд ~ ^лн. а^н +
d$n

+ dtn(r — /Г) + ^Ьсн. а^хн + dmzн-асо2Н.

а*я

Таким образом, получено уравнение типа (1.103) для элемента ло-

_____ £ л

пасти. Оно отличается от последнего слагаемым dtn{r — /г) ——” ,выра­жающим секундную работу силы dtn при маховом движении лопасти, а также тем, что в выражение (1.106) входят составляющие только аэро­динамических сил. Отметим, что уравнение (1.106) может быть также получено приравниванием двух выражений для секундной работы сил элемента лопасти: выражения (1.99) и следующего:

dA = — dQn Ux — dTn [Uy + vr> ] = ~dQn [coHr +

+ Ухийпфп + (r — /Г)0Л (ыхн cos фЛ — <о2няп*л)] —

— dTn [ Уун cos 0n — (r — /r)

+ г(шхишірл + w2Hcos*n)] = — dNa — dXa„ аУи +

+ dTn(r — /r) —————- + dMxH. awxH + dMZK аьз2И. (1.107)

Проинтегрировав (1.106), найдем среднюю по площади винта величину %н. а:

ткн. а~ тпроф + тинд — ^хна^я +

1 2я dfЗп і _ — — _

+ ——- / ———- d фл J dtn(r — /г) + ^хн. а^хн + ^гн. а^гн-

2 п о а1/л о

(1.108)

В прямолинейном установившемся полете интегралы от инерционных составляющих сил и моментов несущего винта равны і нулю, так что ин­дексы а в выражении (1.108) могут быть отброшены. Интеграл от секунд­ной работы махового движения при прямолинейнрм полете также

равен нулю. При криволинейном установившемся Долете в величину

fdtn(T — /г) входит выражение 2(/r + Sr 1Т)(йхн cos фл — со2и sin фл ) о

(см. формулу (1.48) ), так что

d*n fdtn(r ~ І*) =

О

= Ur + 5r/r)(a1wZH + 6іШхн). (1.109)

Правая часть выражения (1.109) совпадает с точностью до знака с выражением для инерционной части крутящего момента несущего винта (1.93) . Таким образом

Первое выражение (1.110) можно получить и по теореме об изменении кинетической энергии. Секундная работа сил элемента лопасти в полу — связанной системе координат

de„

dA = ~dQncoHr + dTR(r — /г) —=

= ~dK + dTn(r — /г)

женного к винту, равна N. Так как при установившемся движении из­менение кинетической энергии за время одного оборота равно нулю, то

Это выражение в безразмерном виде совпадает с (1.110).

Секундная работа моментов инерционных сил несущего винта в соот­ветствии с выражениями (1.97)

тхн. иншхн + т2Я. ИН WZH — (WZH _ UXHW2h) ~ (1-Н2)

так что

^хн. ашхн + тгн. а шгн ~ тхп + тгн шгн • (1.113)

С учетом равенств (1.110), (1.113), а также /хн уравнение

(1.106) обращается в выражение, совпадающее с (1.104).

Итак, мощность несущего винта может быть определена как по выра­жению (1.94), так и по (1.104). Во многих задачах проще использовать выражение (1.104). Дело в том, что приближенные способы определения двух интегралов (1.105) (профильных и индуктивных потерь несущего винта) проще и точнее, чем приближенные способы определения интег­рала в выражении (1.94). Способы определения интегралов (1.105) опи­саны в литературе, например в [10, 17 ], и мы на них останавливаться не будем. Другие величины, входящие в (1.104), это силы и моменты несу­щего винта, которые или определяются в зависимости от Кн, ыхн, toZH, ан, 60, или известны из уравнений движения вертолета. При моделирова­нии движения вертолета, когда вычисленные заранее характеристики винта аппроксимируются, оказывается намного проще аппроксимировать профильные потери несущего винта, чем суммарную мощность. Поэтому в дальнейшем нами будет использовано выражение (1.104), причем про­фильные потери несущего винта будут задаваться графиками (они опи­саны в разд. 1.4.2 и 2.3.1), а индуктивные — вычисляться по формуле (1.122).

Напомним (см. 1.2.1), что нами принят следующий закон распределе­ния индуктивной скорости по площади несущего винта:

чГіф = V[/Tjr1/2/і(и) + (1 + Fcos ФЛ)А (U)h (1-114)

где МО) = 1; /2(0) = 0, а на д > 0,1 = 0; /2 = 1. Таким образом, пер­

вое слагаемое описывает индуктивную скорость на режиме висения, а

второе — на скоростях полета, соответствующих ц > ОД. На режиме ви — сения

"Ъшд = )dtn = V"TJv )dtnrV2. (1.115)

о о

По импульсной теории для кольцевой струйки на режиме висения выполняется соотношение

dT = IdFpv2 = 4itp)rdr — 6np2 r2dr/R. (1.116)

Проинтегрировав (1.117) no 7, получим v2 = T/2*pR2, следовательно,

dT = 3Tr2dr/R3; dtn = 3t~r2 dT. (1.117)

Отметим, что принятое изменение v(r) соответствует распределению циркуляций по закону треугольника и квадратичному закону изменения тяги лопасти. Подставим (1.117) в (1.116)

«инд = 3VTs *„v }rs,2dF~ 1,05v. (1.118)

о

С учетом окружной индуктивной скорости (см. разд. 1.2.1)

^инд * 1>07/Hv.

Для второй составляющей выражения (1.114), т. е. при поступатель­ном полете

«инд = — / d^a + г cos фл) =

2п о о

= vifH + ~ /* cos f dtnr. (1.119)

2п о о

Маховое движение лопастей влияет на распределение элементарной тяги лопастей таким образом, что выполняется условие (см. (1.48) при

1г — * = d^JdK = 0):

1 _ — d2fi

ldtnT — 7г(-Т-Т + 0л) — 2(шхнсо8^л — С02Н5ІП^Л). (1.120)

о 4*л

Очевидно, что с учетом соотношения (1.120) тинд = V(‘H “ 7rWXH)-

so

Таким образом, при прямолинейном полете вертолета характерное для несущего винта распределение поля индуктивных скоростей по зако­ну v(l + rcost/Zjj) (см. рис. 1.5) не приводит к увеличению индуктивных потерь несущего винта по сравнению с равномерным распределением vr ^ = у = const. При криволинейном полете тин’д изменяется на вели­чину 1Г (Ьхн, которая при Гн > 0,15 невелика, но при малых tH, напри­мер при fH = 0,l, сохн =-0,02, увеличивает тинд на 50 %. Из-за отли­чия принятого закона распределения индуктивных скоростей от факти­ческого увеличим найденные значения тинд на коэффициент Ф. С уче­том концевых потерь и в соответствии с формулами (1.114), (1.118), (1.121) получим

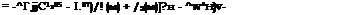
ИНД

(1.122)

Для несущих винтов с обычными для вертолетов геометрическими характеристиками Ф= 1,05, В — 0,98.